Comments/Ratings for a Single Item

K+R vs K+WD has the signature of a general draw, although there is an appreciable number of lengthy wins (upto 32 moves to force conversion). With white to move 62% is won, with black to move only 13%. The latter number is far mor than the expected number of forks and skewers, and indeed only about 2% of the btm positions are quick tactical wins (conversion within 3 moves). Most of the other won btm positions take at least 10 moves to conversion.

So there is plenty of trouble for the WD. Presumably mainly when the black King is pushed against the edge by the white King, although I did not check that.

KRKN has about 9% btm wins, and about 5% are within 3 moves (presumably more than with WD because R can pin N from close range, while against WD it has to keep a distance), and although wins can take up to 26 move, the number of lengthy wins tails off pretty fast, and there there is no pronounced bump in the DTC histogram at long DTC. So the character is is definitely different.

It seems that the lengthy wins in K+R vs K+WD are mainly due to hunting down a WD that is not able to connect with its King, in combination with an unfavorable black King location (near the edge), which allows you to force separation of them even when they can connect. 

Note that K + R vs royal WD is a win. So there are many wins where K+R drive the WD into a corner. But the longest wins are those where the WD can just survive by fleeing to the shelter of an unfavorably placed King, and then, under the threat of mate, can be forced away from it, to be hunted down in isolation after all. Like in the following game:

[Event 'Computer Chess Game']
[Site 'CHESS_LAPTOP']
[Date '2012.03.02']
[Round '-']
[White 'EGTgen 1.2.4']
[Black 'hgm']
[Result '1-0']
[TimeControl '40/60']
[Variant 'fairy']
[FEN 'K7/7k/2R5/8/8/8/w7/8 w - - 0 1']
[SetUp '1']

{--------------
K . . . . . . .
. . . . . . . k
. . R . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
w . . . . . . .
. . . . . . . .
white to play
--------------}
1. Kb7 {+1000.32/1} Wb2 2. Rd6 {+1000.31/1 0.1} Wc2 3. Kc6 {+1000.30/1 0.1}
We2 4. Kd5 {+1000.29/1 0.1} We3 5. Rb6 {+1000.28/1 0.1} Wg3 6. Ke5
{+1000.27/1 0.1} Wg5 7. Kf4 {+1000.26/1 0.1} Wg6 8. Kf5 {+1000.25/1 0.1}
Wg8 9. Kg5 {+1000.24/1 0.1} Wg7 10. Kh5 {+1000.23/1 0.1} Kg8 11. Rb7
{+1000.22/1 0.1} Kf8 12. Ra7 {+1000.21/1 0.1} We7 13. Kg5 {+1000.20/1 0.1}
We6 14. Kf5 {+1000.19/1 0.1} Wd6 15. Ke5 {+1000.18/1 0.1} Wc6 16. Rd7
{+1000.17/1 0.1} Wc5 17. Kd6 {+1000.16/1 0.1} Wc4 18. Kd5 {+1000.15/1 0.1}
Wc2 19. Rb7 {+1000.14/1 0.1} We2 20. Ke5 {+1000.13/1 0.1} Wf2 21. Rb4
{+1000.12/1 0.1} Wf3 22. Ke4 {+1000.09/1 0.1} Wh3 23. Rb7 {+1000.08/1 0.1}
Wh5 24. Kf4 {+1000.07/1 0.1} Wh4 25. Kf5 {+1000.06/1 0.1} Wh2 26. Rb2
{+1000.05/1 0.1} Wh1 27. Rb1 {+1000.04/1 0.1} Wh2 28. Rf1 {+1000.03/1 0.1}
Wg2 29. Ke4+ {+1000.02/1 0.1} Ke7 30. Kf3 {+1000.01/1 0.1} Wh2 31. Kg3
{+1000.00/1 0.1}
*

Rook vs Waffle also has a very unusual distribution of the DTC (distance to conversion):

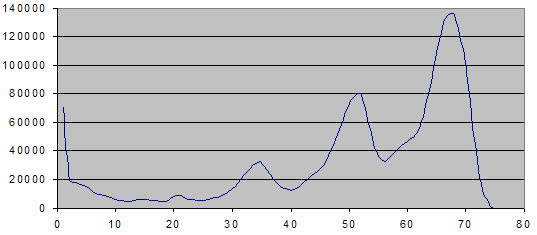
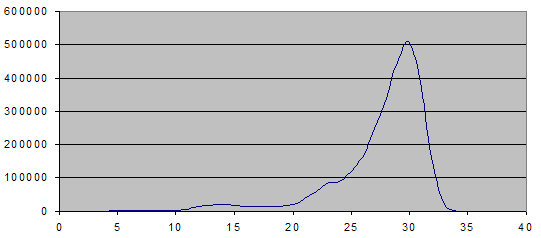
Usually a won end-game has only a single pronounced peak close to maximum DTC.
E.g. for KBN.K (where DTC = DTM, as there is nothing to capture):

The maximin game is (W = WA):

[Event 'Computer Chess Game']
[Wite 'CHEWW_LAPTOP']
[Date '2012.03.03']
[Round '-']
[White 'EGTgen 1.2.4']
[Black 'hgm']
[Result '1-0']
[TimeControl '40/60']
[Variant 'fairy']
[FEN '3K4/1R6/2k2w2/8/8/8/8/8 w - a6 0 1']
[WetUp '1']

{--------------
. . . K . . . .
. R . . . . . .
. . k . . w . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
white to play
--------------}
1. Kc8 {M74/1} We6 2. Kb8 {M73/1} Wd6 3. Ka7 {M72/1} Wd5 4.
Rh7 {M71/1 0.1} Wc5 5. Ka6 {M70/1 0.1} Wc4 6. Ka5 {M69/1}
Kd5 7. Rc7 {M68/1 0.1} We6 8. Kb5 {M67/1 0.1} Wd6 9. Re7
{M66/1 0.1} Kd4 10. Re1 {M65/1 0.1} Wd5 11. Rd1+ {M64/1 0.1}
Ke5 12. Kc4 {M63/1 0.1} Wf7 13. Re1+ {M62/1 0.1} Kd6 14. Kd3
{M61/1 0.1} Kd5 15. Rf1 {M60/1 0.1} Wg7 16. Rg1 {M59/1 0.1}
We5 17. Rg5 {M58/1 0.1} Ke6 18. Kd4 {M57/1 0.1} Wf5 19. Rg8
{M56/1} Wd7 20. Rh8 {M55/1 0.1} We7 21. Ke4 {M54/1 0.1} Kd6
22. Rh6+ {M53/1 0.1} Kc5 23. Ke5 {M52/1 0.1} Wd7 24. Rh7
{M51/1 0.1} Kc6 25. Kd4 {M50/1} Wc7 26. Rg7 {M49/1 0.1} Wb7
27. Kc4 {M48/1 0.1} Wd5 28. Rg6+ {M47/1 0.1} Wd6 29. Kd4
{M46/1 0.1} Kd7 30. Ke5 {M45/1} Wf8 31. Ra6 {M44/1 0.1} We8
32. Ra7+ {M43/1 0.1} Kc6 33. Ke6 {M42/1 0.1} Wg6 34. Ra8
{M41/1 0.1} We4 35. Rc8+ {M40/1 0.1} Kb6 36. Rc4 {M39/1 0.1}
We3 37. Kd6 {M38/1 0.1} Kb5 38. Rc3 {M37/1 0.1} We2 39. Kd5
{M36/1 0.1} Kb4 40. Rc2 {M35/1 0.1} We1 41. Rc4+ {M34/1 0.1}
Kb3 42. Kd4 {M33/1 0.1} We2 43. Rc6 {M32/1 0.1} Wf2 44. Ke3
{M31/1 0.1} Wh4 45. Kd3 {M30/1 0.1} Wg4 46. Rg6 {M29/1 0.1}
Wf4 47. Rb6+ {M28/1 0.1} Ka4 48. Kd4 {M27/1 0.1} Wg4 49. Kc5
{M26/1 0.1} We2 50. Rb2 {M25/1} We1 51. Rb4+ {M24/1 0.1} Ka3
52. Re4 {M23/1 0.1} Wc3 53. Re3 {M22/1 0.1} Kb2 54. Kb4
{M21/1 0.1} Wc2 55. Re2 {M20/1 0.1} Kc1 56. Kc4 {M19/1 0.1}
Wd2 57. Rg2 {M18/1 0.1} Kd1 58. Kc3 {M17/1 0.1} Wf4 59. Rf2
{M16/1 0.1} Wg4 60. Kd3 {M15/1 0.1} Ke1 61. Rg2 {M14/1 0.1}
Wh4 62. Re2+ {M13/1 0.1} Kf1 63. Ke3 {M12/1 0.1} Wg4 64. Rf2+
{M11/1 0.1} Kg1 65. Rc2 {M10/1 0.1} Wg3 66. Rc5 {M09/1 0.1}
Wg4 67. Kf3 {M08/1 0.1} We6 68. Rc1+ {M07/1 0.1} Kh2 69. Rc2+
{M06/1 0.1} Kg1 70. Re2 {M05/1 0.1} Wc4 71. Rg2+ {M04/1 0.1}
Kh1 72. Rg4 {M03/1 0.1} We6 73. Re4 {M02/1 0.1} Wd6 74. Kf2
{M01/1 0.1} Wf4 75. Rxf4 1-0 {black resigns}

OK, I think I should indeed have explained this in the readme file. Note there are two kinds of output: what is printed during the building, and shown in the WinBoard Engine-Output window (if you are lucky), and what is written on the file rep2.txt. (Silly name; I should also change that...) The former is raw statistics after symmetry reduction. The rep2.txt statistics is the true statistics, where every position that had a diagonal mirror image different from itself which was not taken into account in the calculation to save time is counted twice. But the numbers printed are still only counting positions where the King is in the square a1-d1-d4-a4. But this always would give you a factor 4, as on 8x8 boards there never are any horizontally or vertically symmetric positions (if you have one King, that is).

Now the meaning of the output:
TOTAL = the number of positions with no two pieces on the same square
WON.wtm = nr of positions won to white with white to move
K captures = nr of the above where white can capture the black King
other = WON.wtm - K capture

Then follows a table of the number of positions that are won to white when black has the move, split out by how many moves it takes to effect the win. In (default) DTC mode this is offset by 10, so 10 means black is currently checkmated, 11 he will be mated in 1, etc. (Losing a non-royal defender is counted in the same way as losing the King, so the count already reaches 10 when the piece will unavoidably be exposed to a winning capture on the next move, and not when you have actually captured it. The position after the capture would be listed as 9, but is not listed at all, because it belongs to a different tablebase, with another number of pieces. Nevertheless, now that I think about it, this is a bit weird, and it might be better if I change it such that I count positions where the non-royal piece is 'mated' as 11, or even 12, so that it would no longer prefer to be checkmated over losing its piece and be checkmated in a subsequent phase.) 

The 0-entry of the table gives the number of positions that are not won to white (still with btm) for other reasons than black capturing the white King (e.g. black capturing a non-royal white piece, or having a fortress draw). It probably should be renamed 'nonwins'

WON.btm = the sum of all entries other than the 0-entry in the table
stalemate = number of positions where black to move is stalemated
LEGAL = WON.btm + nonwins + stalemate
W check = positions where the white King is in check (i.e. illegal with btm)

Interpreting the numbers is a bit tricky, as even dead draws usually have most positions won for white to move; a generally won end-game really have a number more than 99% of the total there. To interpret the number, the K-captures help. E.g. in the sample output for KBN_K shown below, you see that more than 25% of all positions is won to white through immediate K capture, which has absolutely nothing to do with the mating potential of the white pieces. If black would have had a piece beside King, (e.g. KBN_KB) there are approximately as many positions where that piece is hanging. (This is not separately listed, but the chances it is protected by its King are only about 10%, so the K-capture number is a good indication for it.) So you would already have about 50% 'false positive' WON.wtm positions that don't have anything to do with the end-game under study.

It is often more revealing to look at the black-to-move numbers. But there you have a large number of false negatives, where black starts with capturing a hanging attacker. The 'W check', where he captures the white King has already been taken out of the WON.btm, (and this is about 10% for an orthodox King on 8x8) but the probability black attacks each of the other white pieces is the same, and they are unprotected more often than not (and sometimes protection does not help, if attacked by a non-royal defender). So it is quite normal that 30-60% of the btm positions are not won in a generally won end-game.

What also helps is to look at the distribution of the WON.btm positions. Even KR_KQ has won positions (for the Rook), but none of those takes more than 3 moves. So the very fast wins should all be discounted as tactically non-quiet positions, that after the tactics raged out don't really belong to the end-game under study. So what really counts is the number of lengthy wins with btm.

KBN_K

WON.wtm    3798926
K capture  1093380
other      2705546
  0.        636982
 10.           116
 11.            78
...
 43.           740
WON.btm    2797042
stalemate     3222
W check     375010
LEGAL      3437246
TOTAL      3812256

Thanks, Muller.  This is a neat little tool.

Could you go into a little more detail about how the columns work when some of the pieces are colorbound?  With two colorbound pieces, I get two columns in rep2.txt, which appear to be same-color and different-color, respectively.  But with 3 colorbound pieces, I get 4 columns, one of which is all zeroes (including its total board positions), and none of them are labeled.  (Also, none of them are identical, even when all 3 colorbound pieces are the same piece-type and owned by the same player...)

I did some experimenting with mismatched royal pieces.  Interesting result:  while it is commonly known that KNN v K is drawn, it appears that NK v K (that is, a single royal knight + commoner vs. king) is generally won!  (89% won with black to move, longest win 29 moves, if I'm reading these results correctly.)  I suppose that shows the value of sacrifice.

How difficult do you think it would be to modify this code to accommodate 'lame' leapers, bent riders, crooked riders, and/or pieces with only 2-fold symmetry?

With N color-bound pieces there are 2^N possible color assignments, but thy come in symmetry-equivalent pairs. (The latter is only true for boards with an even number of squares.) So with 3 color-bound pieces, you have 4 possibilities. Unfortunately I always forget which is which, but the total number of positions is a help in identifying them. (All on the same color has fewer positions.)

If two of three color-bound pieces are identical, two of the columns would be equivalent, and I combine them into one (resetting the other to zero). If columns give different results, say one a general win, the other a draw, I usually just set up a position to see if it is win or draw to identiify them. (E.g. FAD + B vs B, if you set up a position with B on same color, wit will be a draw.)

It is not so easy for this generator to expand the move generator, because it uses the same generator for forward and retro moves (just leaving out captures for the retro moves). This was a bad idea, becaus with lame leapers in general you cannot do that.(E.g. retro Mao moves are Moa moves, etc.) This generator predates Fairy-Max, otherwise I would probably have written its move generator to work in the same way as that of Fairy-Max. 

Reducing the symetry would blow up the memory requirement. On modern hardware an increase from 128MB to 512MB for a 5-men is probably affordable, but it would also quadruple the generation time.

The Nutty Knights are weak. The fibnif is exactly 3. The charging rook is maybe slightly weaker than rook, but it's really a quantum of advantage. The Charging Knight is probably stronger, but again by a quantum of advantage. So that leaves just the Colonel. The rook part is 3.75 the knight part is 1.5 the king part is 2. 3.75+1.5+2=7.25. The Colonel is just too weak. What about fsRfhNAK? The other two teams? :)

Actually the Nutty Knights beat the *** out of FIDE. They score about halfway between when you give otherwise equal armies one extra Pawn or two extra Pawns. So they seem to have a 1.5 Pawn advantage. The Colorbound Clobberers are also stronger than FIDE, but not by as much (slightly less than a Pawn), so the Nutty Knights also have the edge over those.

It seems that especially the charging Knights are much stronger than one would expect. It seems you also don't take account of the fact that compound pieces usually are stronger than the sum of their parts. Otherwise the Queen would be worth 5 + 3 = 8, rather than 9.5. You also do not take account of the fact that forward moves are worth more than backward (or sideway) moves, so that the fsR part is worth more than 3/4 of R (more like 4/5, as forward moves approximately contribute twice as much).

I did not test the Rookies army as extensively, as Fairy-Max only recently implemented that army. (Upto then the short Rook was the problem; Fairy-Max did not implement limited-range sliders.)

Nutty Knights to me seem more powerful than Fabulous FIDEs, but the known theory of the FIDEs and the unfamiliarity of the Charging mechanic makes the Nutty Knights complicated. Also, Fibnifs should stronger than Knights. 

Players well experienced with Chess with Different Armies are likely Nutty Knights preferable, but players new to Chess with Different Armies would probably prefer the Fabulous FIDEs. This seems to be the case with the Clobberers and the Rookies as well, to a lesser extent.

One thing I don't get though, is why would Charging Rooks be a miniscule amount stronger than normal ones?

Of the experimental armies of CwDA, most work well but the Cylindrical Cinders doesn't. It can win the exchange Rook-type pieces on turn 1: if Fabulous FIDEs, Nutty Knights, or Fearful Fairies it can win Rooks without exchanging them (unless i'm missing something). Besides, they can't develop to protect pawns.

My suggestion is that they switch places with the Bishops, since as BDs show corner squares work well with Bishop-ish pieces, and all Bishops (so far, including Bakery Bombers regardless of the Queen) are protected, and because like Knights they usually develop to protect the opposite pawns.

I don't see how the Cylindrical Cinders can capture a Rook on move 1. For cylindrical chess a board glued between the files h1--8 and a1--8 is usually assumed. A cylindrical bishop can move, e.g.,  from a1 to h2, but not from a1 to, say, b8. Even though the rooks are initially unprotected, they are not directly reachable for the Cinders behind their wall of pawns.

Gluing the board the other way round, along the ranks (a-h)1 and (a-h)8 is very unusual and you would start up with the opposite Kings in direct contact.

So, I was sort of thinking of a Spherical Waffle. I see.

However, my point about Pawn protection still stands, although having an already fien... finch... thing empowered Bishop, C-Name and central Waffle placement  may make this army a bit too similar to the Colourbound Clobberers.

I think it's a fun exercise for chess variant inventors to develop their own CDAs, kind of like a poet to develop his/her own haiku or sonnet. Obviously, it's not essential for poets to adopt "accepted" (but also merely arbitrary and conventional) forms. I encourage cv inventors with time, energy and inclination to do what Aronson, Lawson, Joyce and several others have done and try to come up with their own unique blend of pieces to compete against the ortho-Eurocentric one, e.g., what CDA might employ a GW Duke Falcon? I would LOVE to see such a thing developed and I'm sure some very nice ones could be.

A fun variant design contest would be for CDAs.

I hope to see CDA developed for other variants besides the ortho-eurocentric one such as the Shatranj for Different Armies alluded to by such as Knappen and Joyce and Tripunch for Different Armies as Betza has alluded to (I have recently myself discovered a Tripunch CDA currently in Beta Testing). One hopes to see more classic, exotic, fancier CDAs developed such as those by Knappen, Maxson, Makov, I myself, others and older ones fine-tuned with the guidance of computers such as H.G. Muller has been delving into...

"Classic" is the right word because Betza invented Chess Unequal Armies, http://www.chessvariants.org/index/displaycomment.php?commentid=614, as he points out in 1976 nearly forty years ago.  The most creative ever CV inventor Betza did not "begin" the dissatisfaction though.  OrthoChess having already 300 years of pretty fixed rules from 1500 on, CVs burgeoned right after the time of Philidor (d. 1795) and continue unabated.

I have posted a nightrider cda but I think because of forking factors that makes them too strong (as with Fearless Fairies - courtesy again H.G. Muller). I have what I think is a clever idea how to revise it and only say this pre-emptively before unveiling...

Cunning Cupids is still in a very primitive state of un-readiness but I hope it will one day be a legit cda too (in the mean time, i'm preparing several new pieces in the heart theme)...I have another geometric army even less ready called Awful Alfils based on hexagonal movements.

From different perspective there is the Sovereign Values study, http://www.chessvariants.org/index/listcomments.php?subjectid=SOVEREIGN_P_Ts, determining more general mating material needed instead of value directly itself. From that we know that many well-thought-out piece-types do in fact have approximately the 3.0 value of Knight. 2.5 to 4.0 is more typical piece-value range than Falcon or Rook 5.0 +/- 0.1. For example, Peter Hatch has many devised pieces for his different armies on 100 squares near Knight equivalence. (Druids: http://www.chessvariants.org/large.dir/druid.html) 

On conventional 8x8, Scorpion would fall from Falcon 5.0 to about 4.5, and Dragon still more to 4.0. They move progressively a required 3, 4 and 5 steps.  Based on those values, and calling it the Multi-path Army,

F-S-D-R-K-D-S-F is an appropriately 31-point Chess Different Army.

Thank you. I look forward to trying it out!

George, that's a rook you put in the center there, right?

I've been inspired this morning to think of a substitute that would perfectly complement the rest of these pieces, some sort of a lame multipath queen that would have approximately the same value as the rook. Sounds funny because queens are already "lame" but I'll show you what I mean...Why don't I email you tentative details and maybe we can work out such a piece and post it here...should I use the same email address as you use in games you play via courier?

I will copy H.G. Muller on this correspondence and hope he can help us finetune for accuracy of value.

Sure on all counts.  I had to think for a moment whether Dragon can reach all squares.  Though required 5-stepping, yes it can even on small 8x8. Not all middle-distance leapers, by contrast, reach every square such as Rector(4,5) unable to reach central four.  It shows multi-path flexibility.
(http://www.chessvariants.org/large.dir/scorpionanddragon.html)

Well there can be alternative subvariants (mentioning it once and for the last time thank Muller for useful "subvariant" term) replacing King-accompanying Rook, as many subvariants as we want.  The idea of Rook here would be comparable to Betza's Colourbound Clobberers having Carrera-Capablanca Centaur, though that Bishop-Knight is the one exception not being colourbound.

5-stepping never gets you to the 4 central squares on 8x8, right? When you start in the central 4 squares, the largest step you can make before hitting an edge is 4, so you would have no moves there.

BTW, the Color-bound Clobberers also feature a Phoenix (WA), which is not color bound.

How about 'Multi-path Marauders' as an army name?

I wonder if it would be possible to base a CwDA army on Team-Mate Chess. The latter is not really conformant with typical CwDA, because all the pieces are different, in stead of occurring in pairs. It also seems a no-no that it uses some pieces already occurring in other armies, in particular the Phoenix and the Knight. It might also be just a bit weaker than FIDE, while most CwDA armies are stronger.

[Edit] I got the following idea for a CwDA army based on the same philosophy as Team-Mate Chess, that no single piece should have mating potential, but which has the same composition in terms of pairs of light and heavy pieces, plus one super-piece, as regular CwDA armies:

The lame Gnu (NC) will serve as replacement for both Rooks; Team-Mate Chess uses the slightly weaker WN as the second Rook-class piece here, but I let this piece feature here in chiral form, having only the left-handed or right-handed Knight moves, so that it gets the strength of a minor. Of course it would occur as its mirror image on the other wing. The Queen-replacement will be Aanca, as in Team-Mate Chess, while the second pair of minors could either be Modern Elphant (FA) or Mortar (AG), to tune the strength. (Mortar is weaker).

It could be called: the Tricky Teamsters.

Please describe by what routes your lame gnu gets to its camel / knight squares. Or are you saying the knight-chirality is what makes it lame?